SageMath-övningar på Hensellyft, primitiva rötter, och KRS

def H_L_tree(f, p: int, r: int):

    vert = [(0,0)]
    for j in range(1,r+1):
        fj = f.change_ring(Integers(p^j))
        fzj = fj.roots(multiplicities=False)
        vert += [(z,j) for z in fzj]


    return DiGraph([vert, 
                    lambda u,v: (u[1] == 1 and v[1] == 0) 
                    or 
                    ( (u[1] == v[1]+1) and ((u[0] - v[0]) % p^v[1] ==0) ) 
                   ])

Ej unika hensellyft

Exempel 1, unika lyft

\(x^{^{p-1}} -1 \mod p^r\)

:CUSTOMID: xp-1–1-mod-pr

\(p-1\) nollställen mod \(p\), alla lyfter unikt 

<<H_L_tree>>
p=7
r=4
R.<x> = ZZ[]
f = R(x^(p-1) -1)
H_L_tree(f,p,r).plot(layout='tree')
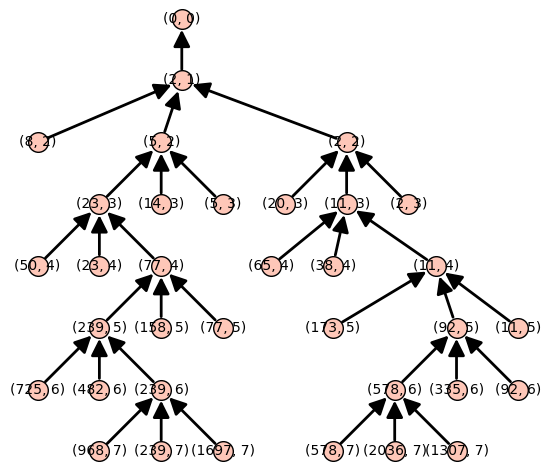
HenselLyftLabHT2023_fig1.png 
<<H_L_tree>>
p=5
r=4
R.<x> = ZZ[]
f = R(x^3+2)
H_L_tree(f,p,r).plot(layout='tree')
HenselLyftLabHT2023_fig1.png 
<<H_L_tree>>
p=3
r=4
R.<x> = ZZ[]
f = R(x^3+2)
H_L_tree(f,p,r).plot(layout='tree')
HenselLyftLabHT2023_fig1.png 
<<H_L_tree>>
p=3
r=7
R.<x> = ZZ[]
f = R(x^4-7*x^3 + 2*x^2+2*x+1)
H_L_tree(f,p,r).plot(layout='tree')
HenselLyftLabHT2023_fig1.png

Har f några rationella rötter? 

f.change_ring(QQ).roots(multiplicities=False)

Vi väljer en rot mod p och lyfter den 

df = diff(f,x)
a=3
dfa=df(a)
df, dfa,f(a), f(a)%p

minv = xgcd(dfa,p)[1]
minv*dfa, minv*dfa % p

y=vector(ZZ,r+1)
y[1]=a
for j in range(1,r):
    y[j+1] = (y[j] - f(y[j])*minv) % p^(j+1)
y

Vi väljer en annan rot och lyfter den 

a=4
dfa=df(a)
df, dfa,f(a), f(a)%p

multiplikativ invers av f’(a) mod p 

minv = xgcd(dfa,p)[1]
minv*dfa, minv*dfa % p

y=vector(ZZ,r+1)
y[1]=a
for j in range(1,r):
    y[j+1] = (y[j] - f(y[j])*minv) % p^(j+1)
y

Övning 1

Välj en tredje rot och lyft den

Större p, fortfarande unika lyft

Hitta nollställena mod pn till följande: 

p=11
r=4
f=(x^(p-1)-1)
f = f.quo_rem(x^2-1)[0]
H_L_tree(f,p,r).plot(layout='tree')
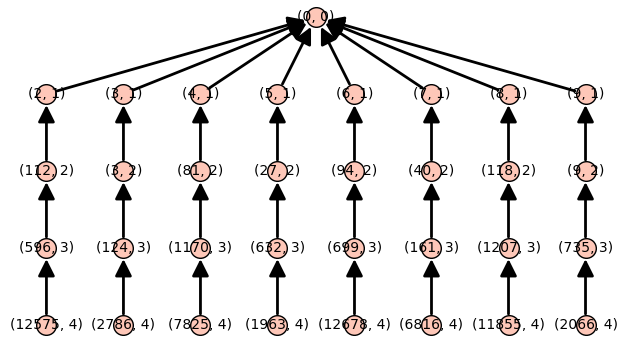
HenselLyftLabHT2023_fig2.png

Övning 2

Har f några rationella rötter? (Ignorera bilden, gör en egen utredning). Välj någon rot mod p och lyft den.

Unika lyft

Exempel 4.21

p = 5
r=4
R.<x> = ZZ[]
f = R(x^3 + x^2 + 29)

H_L_tree(f,p,r).plot(layout='tree')
HenselLyftLabHT2023_fig3.png

Har f några rationella rötter? 

f.change_ring(QQ).roots(multiplicities=False)

Så inga rötter i ZZ, men unika roten mod p lyfter hur högt som helst 

# a=3 enda nollstället mod p=5
df = diff(f,x)
a=3
dfa=df(a)
df, dfa,f(a), f(a)%p

# multiplikativ invers av f'(a) mod p
minv = xgcd(dfa,p)[1]
minv*dfa, minv*dfa % p

y=vector(ZZ,r+1)
y[1]=a
for j in range(1,r):
    y[j+1] = (y[j] - f(y[j])*minv) % p^(j+1)
y

inbyggt kommando, lyfter faktorisering 

fq = f.change_ring(QQ)
fq, fq.hensel_lift(p,3)

-52 % p^3

övning 3

Lyft ännu högre, jämför båda metoderna

Ex 4.23

p = 7
r= 5
f = x^3 + x^2 +2*x + 26

H_L_tree(f,p,r).plot(layout='tree')
HenselLyftLabHT2023_fig4.png

Övning 4

Gör de unika lyften via Hensel!

Icke-unika lyft

Ex 4.22

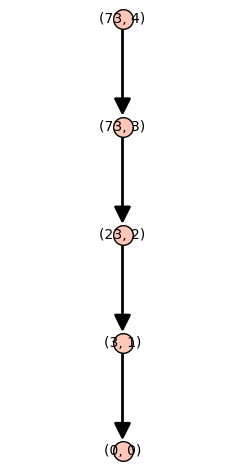
p = 3
r = 6
f = x^2 + x + 7

H_L_tree(f,p,r).plot(layout='tree')
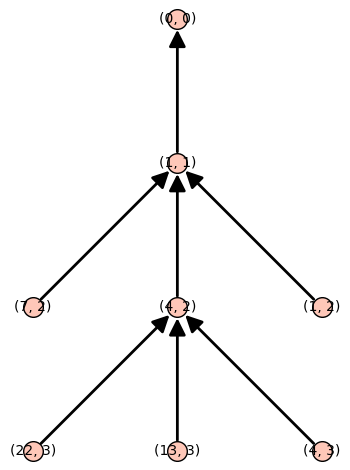
HenselLyftLabHT2023_fig5.png

Övning 5

Så finns lösningar upp till mod \(p^3\) men ej mod \(p^4\), varför? Red ut detta, ledning nedan 

# a=1 enda nollstället mod p=3
df = diff(f,x)
a=1
dfa=df(a)
df, dfa,f(a), f(a)%p

dfa % p

Eftersom f’(a) saknar invers mod p så är alla eller inga av lyften nollställen 

y1 = a
y1lyft = [y1 + s*p for s in range(p)]
y2noll = [z for z in y1lyft if (f(z) % p^2) == 0]
y2noll

Alla lyft fungerade! Gå vidare och försök lyfta dessa mod \(p^3\) För vart och ett av dessa så är antingen alla eller inga av dess lyft nollställen mod \(p^3\)

Övning 6

Finns det polynom med icke-unika lyft som trots allt har nollställen mod \(p^n\) alla n, som inte kommer från rationella nollställen?

Allt lyfter inte

Ex: den rationella roten -1 är den enda som lyfter mot oändligheten 

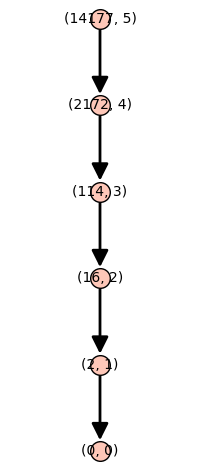
p=3
r=5
R.<x> = ZZ[]
f = R(x^(p^3)  + x^p +2)
H_L_tree(f,p,r).plot(layout='tree')
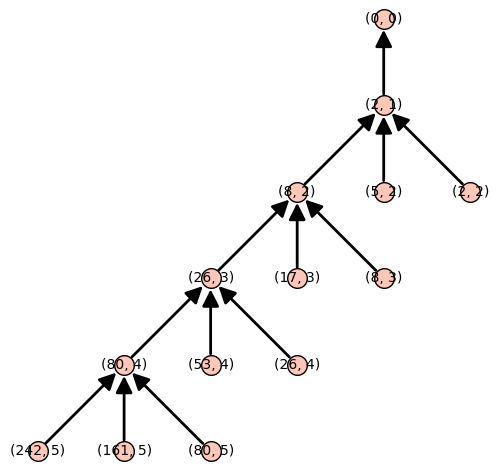
HenselLyftLabHT2023_fig6.png 
# har f några rationella rötter?
f.change_ring(QQ).roots(multiplicities=False)

Den “p-adiska roten” är i själva verket rationell! Kan du ge ett exempel på ett polynom utan rationella nollställen, som har en rot mod p som lyfter icke-unikt mot evigheten?

  • Ledning nedan om du kör fast

    försök med \(p=2\) och \(f=x^3 - 9*x + 8\)

Kvadratrötter mm

# modulo ett udda primtal p så har precis hälften av elementen i
# Z_p^* kvadratrot: om Z_p^* = <g> så har g^(2k) kvadratrötter +/- g^k
# eftersom f=x^2-b har derivata 2x så
# när a^2=b mod p så f'(a)=2a <> 0
# lyfter unikt!

p = 11
r = 5

harkvadratrot = {x^2 % p for x in range(1,p)}
harkvadratrot

p = 7
harkvadratrot = {x^2 % p for x in range(1,p)}
harkvadratrot

a=crt?

a=crt(3,2,11,7)
a

a % 11

a%7

solve_mod?

var('x')

solve_mod([x^2==3],11)

solve_mod([x^2==2],7)

crt(5,3,11,7)

crt(6,3,11,7)

crt(5,4,11,7)

crt(6,4,11,7)

# vi väljer något tal som har kvadratrot mod p
R.<x> = ZZ[]
f = x^2 -3

H_L_tree(f,p,r).plot(layout='tree')
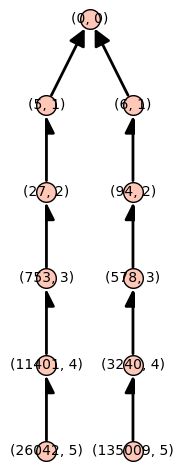
HenselLyftLabHT2023_fig21.png 
# Vi lyfter den ena roten

df = diff(f,x)
a=5
dfa=df(a)
df, dfa,f(a), f(a)%p, dfa % p

# multiplikativ invers av f'(a) mod p
minv = xgcd(dfa,p)[1]
minv*dfa, minv*dfa % p

y=vector(ZZ,r+1)
y[1]=a
for j in range(1,r):
    y[j+1] = (y[j] - f(y[j])*minv) % p^(j+1)
y

# Övning 7
# Gör samma sak för kubrötter!

Färdig rutin

def lift(f, p, k, previous):
    result = []
    df = diff(f)
    for lower_solution in previous:
        dfr = Integer(df(lower_solution))
        fr = Integer(f(lower_solution))
        if dfr % p != 0:
            t = (-(xgcd(dfr, p)[1]) * int(fr / p ** (k - 1))) % p
            result.append(lower_solution + t * p ** (k - 1))
        if dfr % p == 0:
            if fr % p ** k == 0:
                for t in range(0, p):
                    result.append(lower_solution + t * p ** (k - 1))
    return result

def hensel_lifting(f, p, k, base_solution):
    solution = base_solution
    for i in range(2, k + 1):
        solution = lift(f, p, i, solution)
    return solution

p=3
r=5
R.<x> = ZZ[]
f = R(x^(p^3)  + x^p +2)
H_L_tree(f,p,r).plot(layout='tree')

f(2), f(2) % p

hensel_lifting(f,p,r-1,[2])

# Övning 8
# Testa rutinen på något av de tidigare exemplen

Faktorisering av heltal

q1 = nth_prime(200)
q2 = nth_prime(300)
N = q1*q2
p = 7
(N % p,q1 %p, q2 % p)

r = 10
xj,yj=var('xj,yj')
s,t=var('s,t')

solve_mod([s*t == N],p)

# Vi fuskar lite och startar med korrekt faktorisering mod p
xj = 5
yj = 6
j=1
eqn = N - (xj + s*p^j)*(yj + t*p^j)

eqn

eqn2=eqn.expand()
eqn2

eqn3=eqn2 / 7
eqn3

soln_in_st=solve_mod([eqn3],p)
soln_in_st

[(u[0],u[1]) for u in soln_in_st]

soln_in_st[0][0].parent()

niva2lyft=[(xj+u[0].lift()*p^j,yj+u[1].lift()*p^j) for u in soln_in_st]
niva2lyft

(q1 % p^(j+1),q2 % p^(j+1))

# Uppgift 15: skriv en faktoriseringsrutin för tal som
# är prod av två olika primtal.

Primitiva rötter

Primitiva rötter mod p

# Övning 9
# Jag använde följande kod på föreläsningen:
p=nth_prime(362)
print(f'p={p}')
myfact=factor(p-1)
print(f'p-1={p-1}={myfact}')
c=mod(1,p)
C=Set([])
for fact in myfact:
    q,a=fact
    b=a-1
    h=Integers(p)[x](x^(q^a)-1)
    hh=Integers(p)[x](x^(q^b)-1)
    maxl = Set(h.roots(multiplicities=False))
    minl = Set(hh.roots(multiplicities=False))
    candidates = maxl.difference(minl)
    u = candidates[0]
    print(f'primpotensfaktor {q}^{a}')
    print(f'polynom {h},{hh}')
    print(f'nollställen till första: {maxl}, till andra: {minl}')
    print(f'väljer {u} från mängdteodiff')
    c = c*u
    C=C.union(Set([u]))
print(f'multiplicerar ihop {C}, får {c}')
print(f'{c} har ordning {multiplicative_order(c)} borde vara p-1={p-1}' )

# övning 9 forts
# gör om detta till en function nagon_primrot(p: int) -> int
# testa på nth_prime(1000)

# övning 10
# skriv funktion minsta_primrot(p: int) -> int
# testa den, plotta!
# ledning nedan

p = nth_prime(100)
primrotter = [k for k in range(2,p) if multiplicative_order(mod(k,p)) == p-1]
print(euler_phi(euler_phi(p)))
print(primrotter)
primrotter[0]

# övning 11
# Kursboken visar att om p udda primtal, 
# r primrot mod p
# så är antingen r eller r+p primrot för alla p^k
# Implementera detta!
# kombinera till procedur som ger primrot för p^k

# Övning 12
# Skriv en procedur som ger primrot mod n för alla n som har sådan
# testa först

# Övning 13 
# Om finns primrot g mod n så är g generator till Z_n^* 
# som har euler_phi(n) elem
# cycklisk grupp med m elem har euler_phi(m) elem
# så mod n finns euler_phi(euler_pji(n)) elem
# Vad är "average order" för denna funk?

def mystery(n):
    fak = factor(n)
    if len(fak) == 1:
        return(euler_phi(euler_phi(n)))
    elif len(fak) == 2 and fak[0][0] == 2:
        if fak[0][1] <= 2:
            return(euler_phi(euler_phi(n)))
        else:
            return 0
    else:
        return 0

mysterylist=[mystery(k) for k in range(2,500)]
list_plot(mysterylist)

from itertools import accumulate
uppsummeradlista =list(accumulate(mysterylist,operator.add))
list_plot(uppsummeradlista)

Indexaritmetik

p = nth_prime(200)
print(p)
primrotter = [k for k in range(2,p) if multiplicative_order(mod(k,p)) == p-1]
print(euler_phi(euler_phi(p)))
#print(primrotter)
g=primrotter[0]
g = mod(g,p)
g

logtabell = dict([(g^k,k)   for k in range(p-1)])

g.parent()

logtabell[g^3]

logtabell[mod(23,p)]

# Ex 9.19 i boken
p = 17
g=mod(3,p)
logtabell = dict([(g^k,k)   for k in range(p-1)])
[(k,logtabell[k]) for k in range(1,p)]

Kinesiska restsatsen

p1 = 5
p2=11
r=4
R.<x> = ZZ[]
f = R(x^3 + x^2 + 29)

H_L_tree(f,p1,r).plot(layout='tree')
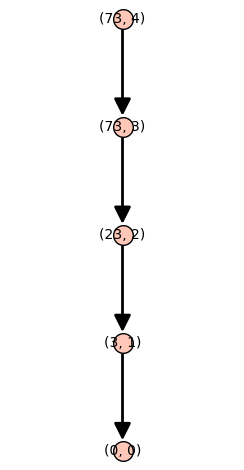
HenselLyftLabHT2023_fig31.png 
H_L_tree(f,p2,r).plot(layout='tree')
HenselLyftLabHT2023_fig33.png 
H_L_tree(f,p1*p2,r).plot(layout='tree')
HenselLyftLabHT2023_fig35.png 
# uppgift 16: kombinera KRT och Hensellyft för att hitta nollställen till f
# mod 55 osv

crt(23,8,p1^2,p2^2)

# Uppgift 16 
# Hitta kvadratrötter mod p1^n*p2^n